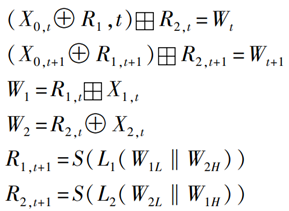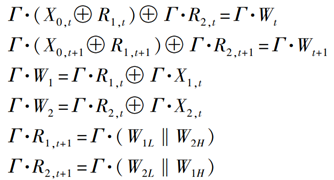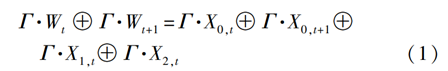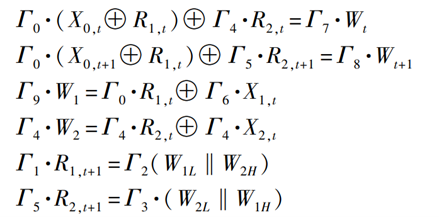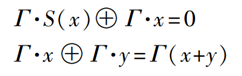安全性讨论

ZUC算法安全性分析的历史

ZUC算法的安全性分析是密码分析中非常热门的问题。目前,针对ZUC算法主要的安全性分析结果如下:

在第一届ZUC国际研讨会上,丁林等人在文献[1]中应用求解特殊的非线性方程思想对ZUC1.4算法提出了猜测决定攻击,计算复杂度是2403,并需要9个密钥字。

011年,周春芳等人针对ZUCv1.5构造了一条轮数为24的选择IV差分传递链,由于完整的ZUCv1.5的初始化轮数为33,因此选择IV差分攻击对ZUC算法的安全性不会构成威胁。 2013年,文献[2]将ZUC算法中基于32比特字的非线性函数转变成基于16比特半字的非线性函数,并对ZUC算法提出了基于16比特半字的猜测决定攻击,这种条件下,计算复杂度是2392,需要9个32比特的密钥字。

2014年,文献[3]指出嵌入式设备执行ZUC加密运算时侧信道信息泄露等问题,并提出了一种基于傅里叶变换的侧信道频域攻击,实验证明该攻击比时域攻击更加有效。

本文利用线性区分攻击方法评估ZUC算法的安全性。线性区分攻击分析方法[4-5]通过对密码算法的非线性部分进行线性逼近,获得只有输出密钥流的线性区分器,以区分真正的随机序列。该方法已经成为判断密码性质好坏的安全标准。因此一个好的序列密码算法应该可以抵抗线性区分攻击。

线性区分攻击原理

2002年Coppersmith等专家提出“区分攻击(Distinguishing attack)”,其目的是判断生成的密钥流序列是否是真随机序列。当为密钥流生成器建立了区分器,并输入一断二进制序列时,会产生两个回答中的一个,这两个回答分别是“该序列是由密钥流生成器生成的”和“该序列是真随机序列”。事实上,该方法并不是一种攻击方式,而是一种判定序列密码性质好坏的安全标准。区分攻击的关键是构造区分器。构造区分器的一个基本思想是对非线性操作部分用一种“特殊路径”进行线性逼近,线性逼近的结果是获得只含有密钥流符号的方程。线性区分攻击吸收了线性分析[6-7]及区分攻击的思想,该攻击方法主要基于下述定义及定理。

对ZUC算法的线性区分攻击[8]

对ZUC算法的线性区分攻击主要有以下3个步骤。

步骤1 将密钥流生成器KG划分为线性部分和非线性部分。线性部分的线性定义如下

Code

1	ϕ(s,t)=⊕¦jcjst=0,cj∈GF(2)

式中:{st+j}j表示线性部分的内部状态。
步骤2 对非线性部分进行线性逼近,得到最优的线性逼近表达式

Code

1	⊕¦jΓi·st+i=⊕¦kΓ′k·zt+k

式中:{zt+k}k为输出密钥流,{Γi}i和{Γ′k}k为32比特掩码Γi·st+i为掩码Γi和状态st+i在GF(2)上的内积。定义上式成立的概率为p,则定义等式偏差ε=1/2-p。如果等式成立的偏差为ε,则大约需要ε-2轮输出密钥流就可以与真正的随机序列区分开。
步骤3 由上述线性逼近表达式构造只包含输出密钥流的线性逼近表达式,并用堆积定理计算该表达式的偏差

Code

1	0=⊕¦iΓi·ϕ(s,t+i)= ⊕¦jcjf(s,t+j)= ⊕¦jcjg(z,t+j)

按照上述步骤对ZUC算法具体攻击过程如下所示。

线性逼近非线性函数F

对ZUC算法在t时刻和t+1时刻,非线性函数F的状态转移函数有：

若存在32比特的线性掩码Γ,用比特‘⊕’ 代替所有的运算(模加和S盒运算),则F的状态转移函数变为

以上6式相加,则有

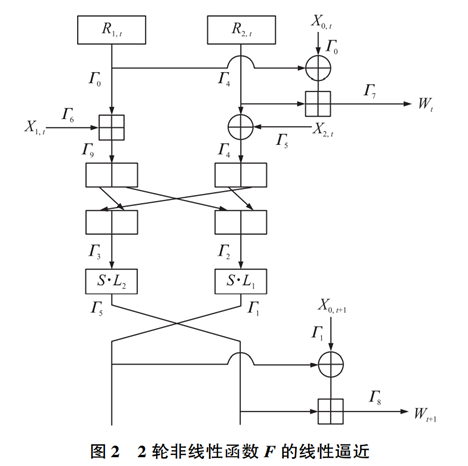
ZUC共有3个模加操作和1个S盒,假设这6个非线性表达式相互独立,则相关性为c+(Γ;Γ,Γ)3cs(Γ,Γ)。为了提高式(1)线性逼近偏差的精度,采用不同的线性掩码Γi,如图2所示;若存在32比特的线性掩码Γi(0≤i≤8),用比特异或‘⊕’代替所有运算(S盒运算和模加运算),F的状态转移函数式对应的线性逼近表达如下:

从上面线性逼近过程可知,当满足条件Γ4=Γ2L‖Γ3H和Γ5=Γ3L‖Γ2H时,将上述6个线性逼近表达式相加，消去中间变量W1、W2、R1,t、R1,t+1、R2,t、R2,t+1,得到关于输入变量X0,t、X0,t+1、X1,t和X2,t与输出变量W1、W2的线性逼近关系Γ0·X0,t⊕Γ1·X0,t+1⊕Γ6·X1,t⊕Γ4·X2,t=Γ7·Wt⊕Γ8·Wt+1 (2)
计算式(2)的偏差:式(2)中含有两个非线性操作分别为3次的模232加运算和1次S盒变换。搜索非线性函数F的线性逼近表达式来自于搜索

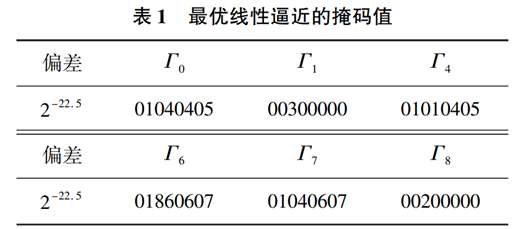
定义它们的偏差为εs(Γ)和ε+(Γ),则非线性函数F的偏差为εF(Γ)=2·εs(Γ)·23-1·ε+(Γ)3。在本文的实验中只使用一个激活的S盒,来获取线性逼近方程式(1)的最大偏差。如何搜索6元组掩码(Γ0,Γ1,Γ4,Γ6,Γ7,Γ8)使得式(1)成立的最大偏差。如果本文要遍历所有的32比特掩码值,在现实生活中是不符合实际的。事实上,一般会选取汉明重量相对较低的掩码值。由文献[9]得到的掩码值如表1所示。

根据堆积引理,可计算出区分器的线性偏差ε=23-1ε3 F≈2-65.8
因此,利用本文提出的线性区分攻击方法,需要N≈1/ε^2 =2131密钥流比特,ZUC就可以被区分,同时需要的计算复杂度为2131,利用定理2,当密钥流比特N≈1/ε^2 =2131时,该区分攻击的区分优势为0.38。综上所述,该区分攻击需要约2131比特密钥流就能以0.38的区分优势把流密码ZUC与随机序列区分开来。当密钥流比特大于131时,密码算法是不安全的；但对于只有128比特密钥的ZUC算法,该结果超过了密钥流序列的长度,因此我们再次证明了ZUC算法是安全的。

Code

[1] Ding L, Liu S K, Zhang Z Y, et al. Guess and determine atack on ZUC based on solving nonlinear equations [J]. Proc of the Record of the 1st Int’l Workshop on ZUC Algorithm,2010,26(6-7):1-8. 
[2] 关杰,丁林,刘树凯. SNOW3G 与 ZUC 流密码的猜测决定攻击[J].软件学报,2013,24(6):1324-1333.Guan Jie,Ding Lin,Liu Shukai. Guess and determine attack on SNOW3G and ZUC[J]. Journal of Software, 2013,24(6):1324-1333.
[3] 唐明,高剑,孙乐昊.嵌入式平台下ZUC算法的侧信道频域攻击[J].山东大学学报,2014,49(9):29-34.Tang Ming,Gao Jian,Sun Lehao. Side channel attacks in frequency domain for ZUC algorithm in embedded platform [J].Journal of Shandong University,2014, 49(9):29-34
[4] 刘志强. 分组密码的线性类分析方法研究[D]. 上海:上海交通大学计算机学院,2011. 
[5] 连至助. 序列密码的设计与分析研究[D]. 西安:西安电子科技大学计算机学院,2011.
[6] 李顺波,胡予濮.eSTREAM候选算法的区分攻击研究[D].西安:西安电子科技大学计算机学院, 2012:45-48. 
[7] 刘艳,潘丰.线性离散系统Delta域控制器设计[J].南京理工大学学报,2015,39(5):571-577. Liu Yan, Pan Feng. Controller design for linear discrete-time system in delta-domain [ J]. Journal of Nanjing University of Science and Technology,2015, 39(5):571-577.
[8] 汤永利,韩娣,闫玺玺,叶青,李子臣.祖冲之序列密码的线性区分攻击分析[J].南京理工大学学报,2016,40(4):452-454.Tang Yongli,Han Di,Yan Xixi,Ye Qing,Li Zichen. Linear distinguishing attack analysis on ZUC stream cipher[J]. Journal of Nanjing University of Science and Technology,2016,40(4):452-454.
[9] Cid C, Murphy S, Piper F, et al. ZUC algorithm evaluation report [ R ]. London: Codes & Ciphers Ltd. ,2010.

安全性讨论

ZUC算法安全性分析的历史

线性区分攻击原理

相关定义

对ZUC算法的线性区分攻击[8]